
『TAKEのIT風万記』というサイト名ですが、この記事はITに携わらない方にも学びがある記事なので、ぜひご活用ください!

対偶ってなんだっけ?
対偶とは、仮定と結論を否定し、その順序を逆にしたものです。
例えば
『雨が降れば、道が濡れる』
という命題があった時、その対偶は
『道が濡れていなければ、雨は降っていない』となります。

なるほど!
それぞれ否定して、順番をひっくり返すんだね!

でもこれが人生でどう使えるの??
対偶の考え方を使うと、別の視点から物事を考えられるので、新しい発想や、アイデアが出てきやすくなります!
では早速見ていきましょう!
命題と真偽のおさらい
命題とは?
式や文章で示された事柄で、正しいか正しくないかが明確に決まることを命題と言います。
例えば
『人間は動物だ』は命題ですが
『人間は大きい』は命題ではないです。

誰が見ても、正しいか正しくないかがはっきりするのが命題なんだね!
真偽
命題が正しい状態を、「真」
命題が正しくない状態を「偽」と言います。
例えば『雨が降れば道が濡れる』は真でしょうか?偽でしょうか?
雨が降れば必ず道は濡れるので、これは真だと言えます!
命題とベン図
ベン図

ベン図?
聞いたことあるような...
ベン図は「集合」を図で表現する方法の一つです。
「集合」についての説明は割愛します。
何かの集まりという認識で大丈夫です。
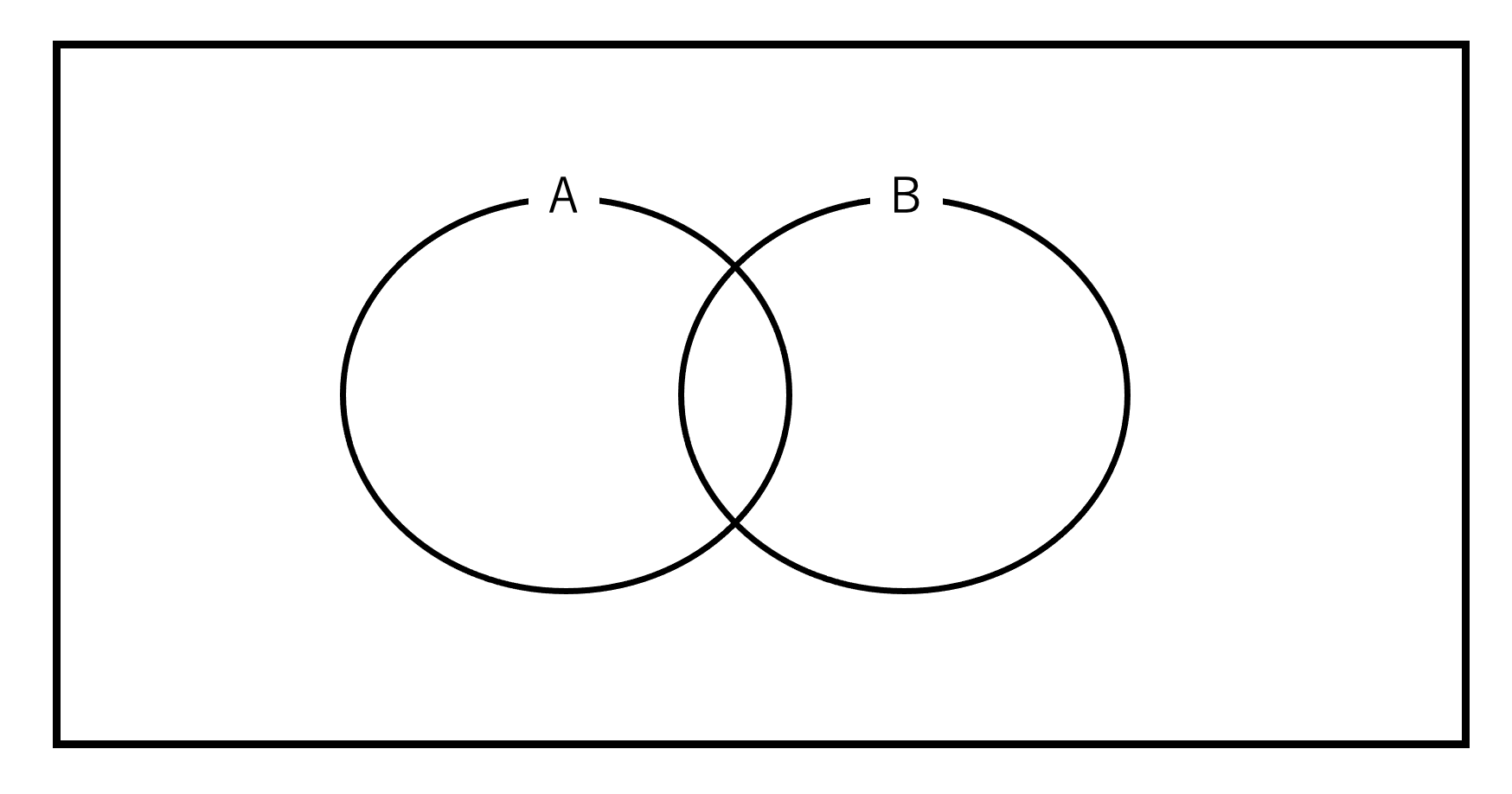
命題とベン図の関係

ベン図は見覚えがあったけれど
一体これが命題とどういう関係があるの?
実は、命題はベン図で表すことができるのです。
『雨が降れば道が濡れる』をベン図で表してみましょう!
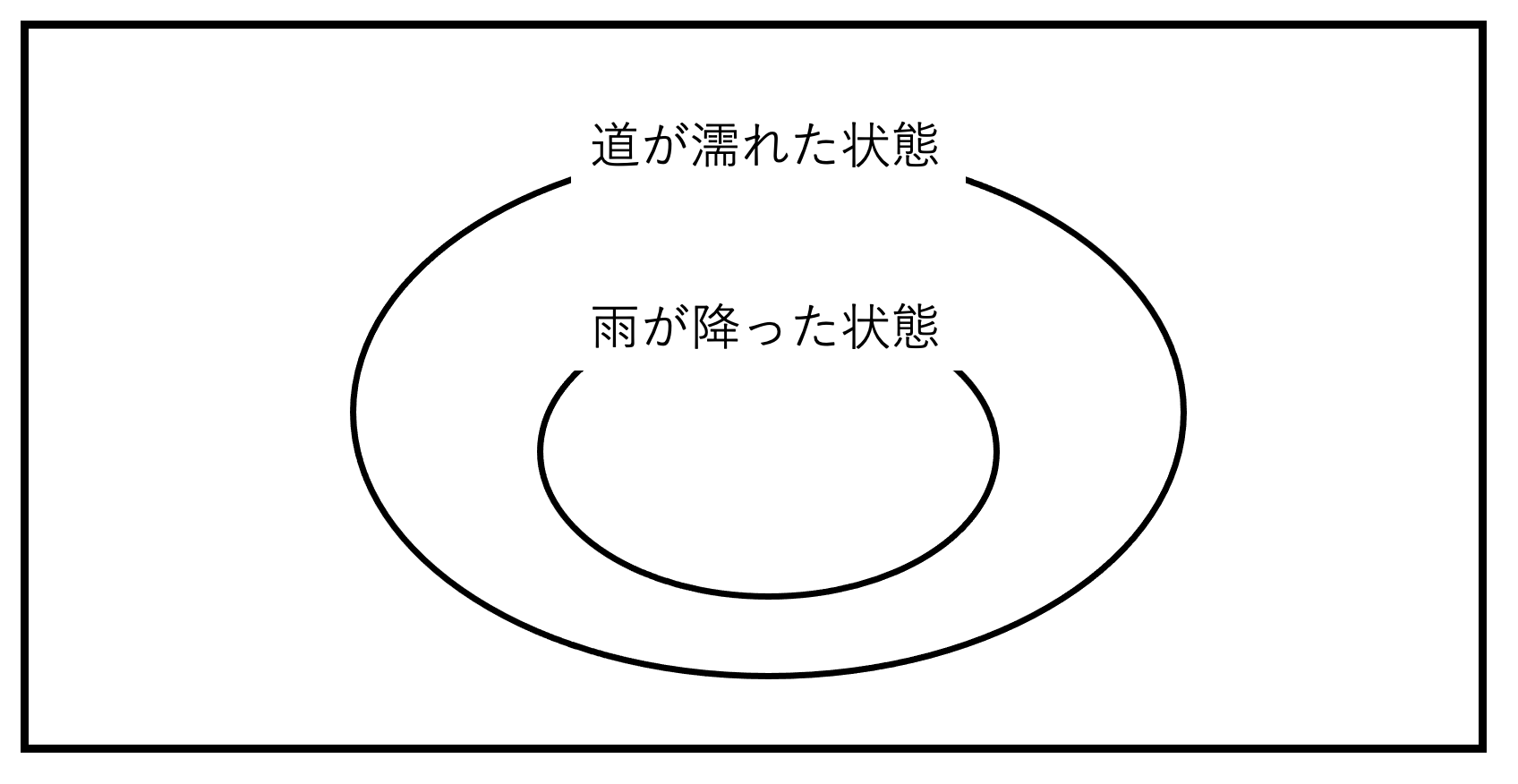

「道が濡れた状態」の丸の中に「雨が降った状態」の丸が入ってるよ!?
丸が別の丸の中にすっぽり入っていても大丈夫です。
これもちゃんとしたベン図です。
そして注目して欲しいのが、雨が降った状態の丸にいる時、必ず道が濡れた状態の丸の中にいます。
なので、『雨が降れば道は濡れる』という命題が真と言えるのです。

ほんとだ!
そう言われると絶対に真になるね
命題・対偶・ベン図
対偶とベン図

で、そろそろ対偶に戻ってください!
では対偶に戻ります。
元の命題の仮定と結論を否定して、順番を逆にした命題を対偶の関係と言いました。
つまり、命題の対偶も命題なのです。
従って、命題がベン図に表せられるなら、命題の対偶もベン図に表せられます!
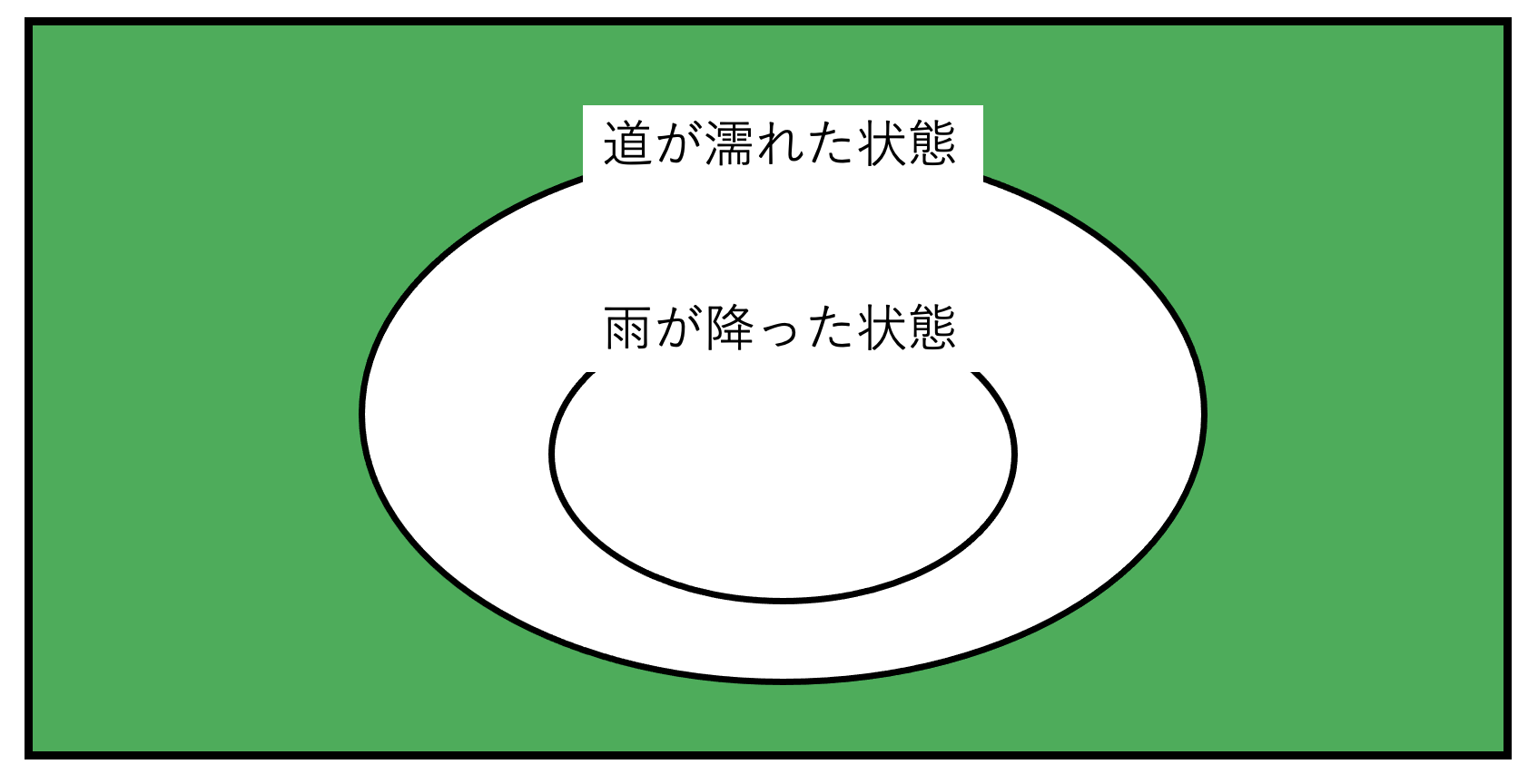

緑色が増えただけ?
緑色の部分は「道が濡れた状態ではない」ってことだから...
そうです。緑色の部分は「道が濡れた状態ではない」つまり、
「道が濡れていないければ」に該当します。
そして注目して欲しい部分は
緑色の部分は「雨が降った状態ではない」ということです。

言われてみればたしかに!!
命題・対偶
結論として言いたいことは、
対偶は、元の命題と必ず真偽は一致するということです。
理由はベン図を見れば一目瞭然です。

元の命題が真であれば、対偶も真になって
対偶が真なら、元の命題も真になるのね!
対偶の考え方を活かす
対偶を活用する

対偶は理解したけれど、結局何に使えるの?
アイデアや考え方の発想の転換に活用できます。
例えば
私は最近だと、「タイピングが速い人は何をしているのか?」と悩みました。
そこで
「キーボードを見ずにキーボードを打つと、タイピングが速い」という命題を考えました。
これは真なのでしょうか?
(速いというのは定性的なので、正しいか正しくないかの基準が不明確で、厳密には命題とは言えないですが...)

タイピングが速い人はキーボードを見ていないので、これは「真」です!
ところが
上記の対偶を考えて、発想を転換させると、
「タイピングが遅いのは、キーボードを見て入力するから」となります。
これは真なのでしょうか?

キーボードを見た方がタイピング自体は速くなります...
これは「偽」なのでは?
そうです。
そして対偶が「偽」なので、元の命題も「偽」になります。
よって、
「キーボードを見ずにキーボードを打っても、タイピングは速くならない」とわかりました。

対偶を使えば、別の角度から物事を考えることができるね!
なので、結論づける前に「対偶」を考えてみると意外な答えが見つけることができます!

また、「キーボードを見ずに打てる人は、タイピングが速い人」
は真になります!ぜひ対偶を考えてみてください!
最後に
今回は「対偶」を使って、別の角度から物事を見る方法をお伝えしました。
仮定と結論があった時、すぐに結論づける前に、その対偶を考えてみてはどうでしょうか!
それだけでかなり結論の精度が上がります!

結論づける前に一手間。だね!
その通りです。
ぜひ「対偶」の考え方を活かして日々の業務に活かしてみてください!